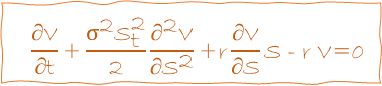
Que es un Portafolio o Cartera de Inversión
Un portafolio o cartera de inversiones es un conjunto de activos financieros que pertenecen a un inversionista. Este puede incluir bonos, acciones, derivados, monedas, efectivo, materias primas y muchos activos más.
Los elementos de un portafolio varían su valor a lo largo del tiempo, implicando así que su valor también lo haga. En esta entrada nos centraremos en portafolios bastante sencillos. Compuesto por algún activo financiero, que permita algún tipo de opciones sobre este, y que contiene además dichas opciones sobre el activo. Un ejemplo puede ser un portafolio compuesto por acciones y algún tipo de opciones sobre estas.
Como hemos dicho, a lo largo del tiempo el valor del activo financiero varía por lo que el valor de las opciones sobre este no solo se ve afectado por el transcurso del tiempo sino también por el valor del propio activo financiero, llamado también subyacente.
Valor del Portafolio.
Partimos de que tienes un portafolio y el valor de este lo denotamos con la letra P (de portafolio). Este portafolio está formado por una cantidad Δ (que es considerada continua y no necesariamente una cantidad entera) del activo financiero, es decir el subyacente, que hemos comprado. El valor del subyacente lo denotamos con la letra S y este valor varía con el tiempo S = S(t) = S_t .
Además el portafolio contiene una opción (opción Call o Put) con valor V y por lo comentado en el apartado anterior este valor depende tanto del tiempo como del valor del propio subyacente V = V(t,S) .
Entonces el valor de nuestro portafolio varía a lo largo del tiempo teniendo en cuenta también el valor del subyacente P = P(t, S) y se cumple además la siguiente relación:
P=V - \Delta S \qquad(1)
La relación (1) en notación diferencial (decimos en notación, porque S es un proceso estocástico y esto implica que no es diferenciable en el sentido clásico) tenemos que
dP=dV- \Delta dS \qquad(2)
Obteniendo la Ecuación de Black & Scholes
El modelo Black-Scholes supuso para sus creadores Myron Scholes y Robert Carhart Merton el premio Nobel de Economía, Fischer Black falleció antes de la concesión del premio.
Para valorar el precio V=V(t, S) de la opción asumimos que se cumplen los siguientes principios:
- El precio de la acción es un proceso de Ito satisfaciendo la ecuación Lognormal (movimiento Browniano geométrico):
dS = \mu Sdt + \sigma S dW \qquad(3)
- Asumimos que tanto la media μ como la varianza σ son constantes.
- Hay ausencia de arbitraje y el tipo de interés r, es constante por lo que debe ocurrir que
dP=rPdt \qquad(4)
- La fuente de riesgo está determinada por el termino estocástico dS.
Entonces bajo estas hipótesis aplicando el lema de Ito al precio de la opción nos queda
dV=\left(\frac{\partial V}{\partial t}+\frac{\sigma^{2}S^{2}}{2}\frac{\partial^{2}V}{\partial S^{2}}\right)dt+\frac{\partial V}{\partial S}dS \qquad(5)y las siguientes igualdades quedan justificadas por (4) y (1) (la primera) y (2) y (5) (la segunda):
r\left(V-\Delta S\right)dt=dP=\left(\frac{\partial V}{\partial t}+\frac{\sigma^{2}S^{2}}{2}\frac{\partial^{2}V}{\partial S^{2}}\right)dt+\left(\frac{\partial V}{\partial S}-\Delta\right)dS \qquad(6)
La eliminación del riesgo es generalmente denominada “hedging” y si esta eliminación es llevada a cabo utilizando un activo y su subyacente (como es el caso) es entonces llamado “delta hedging”. Queremos entonces que el termino dS no nos quede en nuestra ecuación lo cual se logra si:
\Delta = \frac{\partial V}{\partial S}deduciéndose entonces la llamada Ecuación de Black-Scholes:
\frac{\partial V}{\partial t}+\frac{\sigma^{2}S^{2}}{2}\frac{\partial^{2}V}{\partial S^{2}}+r\frac{\partial V}{\partial S}S-rV=0